지수와 로그의 관계

곱셈을 덧셈으로 바꾸는 식?


위의 식을 곱한 후 2로 나누면 아래와 같은 곱셈이 덧셈으로 바뀐 형태가 되는데, 로그 이전에는 미리 계산된 삼각함수를 이용하여 큰 수의 곱셈을 계산하기 쉬운 덧셈으로 바꿔 계산했다. (실제로는 사인함수를 사용하기도 했다)
573.6 * 29.24 를 계산한다고 하면 0.5736 * 0.2924 * 100000 값과 같은데, 미리 계산된 cos 표에서 근사치를 가져온다.
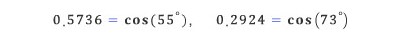
위 두 값을 공식에 대입하면 아래와 같은 값이 나온다.
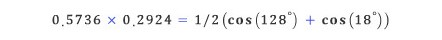
계산된 cos 표를 확인하여 os(128°) = -cos(52°) = -0.6157, cos(18°) = 0.9511 의 값을 가져와 식에 대입하여 계산한다.
결과 값에 100,000을 곱하여 16770 이라는 값을 얻을 수 있다.

실제로 573.6 * 29.24 를 계산하면 16,772.064 라는 값이 나오는데, 계산된 cos 값이 소수 넷째자리에서 반올림한 근사치이기 때문이다.
네이피어의 로그
16세기의 천문학자 티코 브라헤는 삼각함수 계산에 능통했는데, 어느날 자신의 천문대를 방문한 왕자에게 이 계산법을 시연했다. 옆에서 계산법을 유심히 지켜보던 왕자의 주치의 존 크레이그는 이 계산법을 자신의 친구 존 네이피어에게 보여주게 된다. 이후 20년의 연구를 거쳐 로그를 발견하게된다.
조건1. 일정한 길이(1)의 선분인 AB와 무한의 직선인 CD가 있을 때 A, B에 위치했던 P와 Q는 동시에 일정속도(1로 정의)로 출발한다.
조건2. P는 B까지 진행되면서 a가 짧아질수록 P의 속도도 비례하여 줄어들고, Q의 속도는 유지된다.
이때 PB의 길이 a에 대해 x(CQ의 길이)를 a의 로그라고 정의한다. -> LOG(a) = x
*LOG는 네이피어로그
*초기 길이가 1이기 때문에 남은거리는 0<a<1 가 된다. 물론 100,000으로 정의해도 초기 거리보다 작은건 마찬가지
*a는 P의 속도에 비례, 이동거리(LOG(a))에 반비례

P에서 조금 더 시간이 흘러 Q가 LOG(b)만큼 이동했을때의 남은거리(P'B의 거리)를 계산해보자
비례식을 사용하면 길이 1의 선분 AB에서 속도 1로 출발하여 LOG(a)만큼 갔을때 1*a가 남았으니,
길이 a의 선분 PB에서 속도 a로 출발(길이가 a만큼 짧아졌으니)하여 LOG(b)만큼 갔기 때문에 a*b가 남게 된다.

다시 처음으로 돌아와서 A에서 출발한 점 P'가 거리 ab만큼 남았을때 점 Q'는 LOG(a)+LOG(b)만큼 이동한다.
-> LOG(ab) = LOG(a) + LOG(b)
b대신 b/a를 대입하면 LOG(a) = LOG(a) + LOG(b/a)
-> LOG(b/a) = LOG(b) - LOG(a)
LOG(a) 만큼 처음 움직였을때 남은거리는 1*a 였고, 또 LOG(a)만큼 움직였을때 남은거리는 a*a 가 된다. 여기서 한번 더 LOG(a)만큼 움직인다면 a^2에서 남은거리가 a^2*a가 된다.
-> LOG(a^n) = LOG(a) + LOG(a) ... = nLOG(a)
로그를 사용하여 계산하는 방법
2^50 이라는 큰 수는 로그를 이용하면 쉽게 계산할 수 있다.
a^x = y 에서 y를 구하려고 하는 상황인데 양쪽에 log(10)을 해준다.
log(10)2^50 = log(10)y 인데 위의 로그법칙에 의해 50log(10)2 가 되며
log(10)2 = 0.3010 이기 때문에 50을 곱하면 15.0514998... 이 된다.
log(10)10 = 1이고 15 = log(10)10^15 이므로
log(10)2^50 = log(10)10^15 + 0.0514... 가 된다. 0.0514... = log(10)1.12589 이므로
대입하면 log(10)2^50 = log(10)10^15 + log(10)1.12589 가 되고, 위에서 나온 첫번째 법칙에 의해
log(10)2^50 = log(10)10^15 + log(10)1.12589 = log(10)(10^15 * 1.12589)
양쪽의 log(10)을 없애주면 2^50 = 1.12589 * 10^15 가 남는다.
이렇게 두번의 미리 계산된 값을 로그표에서 찾으면 큰수라도 빠르게 계산할 수 있다.
상용로그를 사용하는 이유?
브리그스는 네이피어가 만든 로그에 감탄하여 네이피어와 함께 로그를 편리하게 사용하기 위한 연구를 했다.
미리 계산된 로그값을 가지고 대입하면 큰수의 계산이라도 쉽게 풀 수 있기 때문에 처음엔 모든 밑에 대해 로그값을 계산하려 했지만 비효율적이라고 생각했다.
하지만 log(2)64/log(2)4 = log(4)64 임을 깨닫고 log(a)b = log(c)b / log(c)a 라는 밑변환 공식을 만들어내게 된다.
밑을 자유자재로 변환시킬 수 있으니 사람이 가장 계산하기 편한 10진수를 가지고 log(10) 이라는 상용로그만 계산해두고 나머지는 밑변환 공식을 통해 log(10) 으로 만들어 사용하도록 했다.
자연로그를 사용하는 이유
e?
100%의 성장률을 가지고 1회 연속성장 할 때 가질 수 있는 최대 성장량

100%의 성장률을 가지고 1회 비연속 성장하는 경우 -> 1+1 = 2

100%의 성장률을 3번에 나눠서(33% * 3) 성장하는 경우 -> 1 * (1+1/3) * (1+1/3) * (1+1/3) = 2.370
처음 1원이 1.33원으로 성장하고 또다서 1.33배 증가하고 또 1.33배 증가했다.
같은 100%의 성장률이지만 횟수를 나누면 값이 커진다.
최대 성장률을 보기 위해 100%의 성장률을 무한번 나눠 연속성장 시키는 경우 (1+1/n)^n 이라는 공식이 나오고 e는 이렇게 찾게된것이다.
어떤 값(n)을 100% 성장률로 1회 연속 성장하는 경우 n*e 가 되며,/ 2회 연속 성장하는 경우 e^2가 된다. 또한 50% 성장률로 연속 성장하는 경우 (1+50%/n)^n 이 되며(50%를 무한대로 쪼개야되기 때문에) 이 값은 ((1+50%/n)^2n)^(1/2)과 같기 때문에 e^(1/2) 가 된다.
따라서 e^x 에서 x는 성장률, 성장횟수, 성장량과 관련이 있다.
e를 밑으로 갖는 이유
큰수를 정밀하게 계산하기 위해서는 등비수열의 각 항 사이 사이가 조밀해야 하며, 조밀한 값들이 모두 등차수열에 일대일 대응이 되어야 한다.
https://blog.naver.com/sbssbi69/90159024636
'프로젝트 > 게임 AI' 카테고리의 다른 글
| 인공지능을 위한 수학 level 1 : 변수와 상수 ~ 자연로그 (0) | 2019.08.06 |
|---|---|
| 딥러닝 선수지식 3 : 수학과 파이썬 (0) | 2019.08.05 |
| 딥러닝 선수지식 2 : 파이썬 기초 (0) | 2019.08.03 |
| 딥러닝 선수지식 1 : 딥러닝이란? (0) | 2019.08.03 |



